Experiments
What classifies a task as an experiment? There must be an intervention.
Type of experiment: Comparison
Note 1:
It cannot be a prediction-type task involving scatterplots. For example, dropping a ball at various heights, recording the bounce heights and then using these results to predict a bounce height from a drop height.
Note 2:
The focus is on experiments and exploratory data analysis and not on sampling and sample-to-population inferences.
TOP
Type of design
Two independent group comparison
Note 3:
Do not use word sample, rather use the word group, and note two groups must be independent. The people/objects used do not have to be samples from a defined population. The number of people/objects used should be of a reasonable size so that features of the data can be explored.
There must be random allocation to the two groups in an attempt to make the comparison fair. Students can discuss why.
Analysis: Compare using dot plots and/or boxplots
Students describe what they see. Use mean, sd, median and IQR. Describe shifts, variation, clusters etc. Students should link features of the data to the experiment and seek explanations by exploring the data. Students can make descriptive comments about the size of the difference between the two groups and consistency of the data within each group.
Conclusion is a suggestive inference
For example, these data suggest (appear) that using a fixed target line resulted in (caused) the students jumping further on average than when no target line was used. (This experiment is described later in the examples.)
Note 4:
Noting the difference between descriptive statements and suggestive inference statements.
Example of a descriptive statement: The students who used a fixed target line tended to jump further than the students who did not use a target line.
Example of a suggestive inference statement: For the students in this experiment, this suggests that the use of a fixed target line results in students having a tendency to jump further than when no target line is used.
Note 5:
Where there is a detectable shift (which is most of the time) there is a suggestion of a causal relationship (at level 7). At level 8 this suggestion is investigated further using randomisation methods.
Note 6:
There are two types of inference: causal-type inference and sample-to-population type inference. The conclusion statement of an experiment at Level 7 must at least include a causal-type inference statement as above.
Note 7:
A sample-to-population type inference is not acceptable. For example, a conclusion written as “these data suggest that (all) Year 12 students using a target line tend to jump further than (all) Year 12 students not using the target line” is not acceptable as the conclusion as it does not explicitly express an association-to-causation inference. It does not explicitly give the idea that the target line is the causal agent in this difference.
Paired comparison
Note 8:
Paired comparison is where measurements are taken on the same person or object. You cannot do separate dot plots of ‘before’ and ‘after’ observations and then discuss as if they were not related.
It is keeping the link between the ‘before’ and ‘after’ that means dot plots and box plots are not appropriate graphs to use as the link between paired observations is lost. That is, you don’t see the movement between ‘before’ and ‘after’ in the dot/box plots.
Analysis: New type of plot
(The two examples given showing the same thing.)
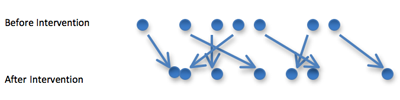
New type of plot_1
Students describe what they see only in terms of the direction of the arrows (i.e., the differences).
New type of plot_2
For example, all but three students stood longer with their eyes open than with their eyes closed, that is, for all but three students the differences are positive.
Followed by dot plots and/or boxplots of the differences, Students describe what they see. Use mean, sd, median and IQR of the differences. Describe shift, variation, clusters etc. of the differences. Compare the differences to 0, which is no change. Students should link features of the data to the experiment and seek explanations by exploring the data. Students can make descriptive comments about the direction (positive, negative), size and consistency of the change in the response variable.
Scatterplots can be used, but they are harder for students to interpret. Would need to discuss relative to the y=x line rather than doing a bivariate analysis as we would do for relationship situations which this is not. That is discussing those results above the line, on the line and below the line.
Conclusion is a suggestive inference
For example, these data suggest (appear) that the caffeine caused the pulse rate in the students to go up on average.
For example, 20 of the 25 students had an increase in pulse rate after having a caffeine intake, i.e., 20 of the 25 differences are greater than zero. This suggests that for these 25 students, the caffeine intake resulted in (caused), on average, an increase in pulse rate.
Note 9:
For both types of experiment students can discuss other relevant factors that they should consider etc.
Note 10:
Notes 3 -7 above also apply to experiments with a paired comparison design.
TOP
Examples of experiments
Random allocation – two independent groups
- Experiment on the effects of light on the growth of radish seedlings. (Franklin et al., 2005, pp. 75-76) This involves randomly allocating radish seedlings to three different light treatments. One treatment is 24 hours light, one treatment is 12 hours light, 12 hours dark and the third treatment is 24 hours dark. See:
GAISE Reports: PreK-12 Report (PDF 400KB)
- Estimating the number of objects in a collection (without counting). Find the difference between the estimate and the number. Have two treatments – large number of objects (say 40) versus smaller number of objects (say 15). Randomly allocate students to the two different treatments.
- Time to write The Quick Brown Fox…, one group using left hand versus other group using right hand (ignoring dominant hand issues – randomisation should take care of that but it allows for an introduction to blocking ideas too).
- Do you get more juice from a citrus fruit if you microwave it for a short time before juicing it? Get a bag of similar sized citrus. Randomly allocate half to get a burst of microwaves and then measure the juice from each fruit. Need to be accurate to the nearest mL or could weigh the juice since electronic scales are easy to come by. Can do lemons, limes and oranges. If you want to get complicated can also use different varieties of lemons. Can do 10, 20 30 second microwaves (depending on strength of microwave).
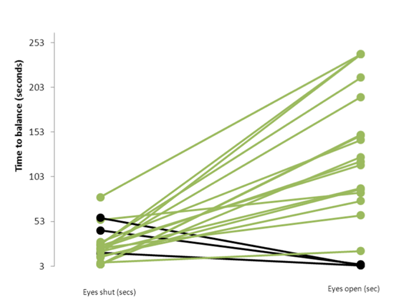
- Time to stand on one leg with both eyes shut versus both open. Randomly allocate participants to eyes shut or eyes open group.
- Pulse rates:
- Sitting or standing – randomly allocate to sitting or standing
- Stepping up and down, one step size versus a bigger step size – randomly allocate to one step size or the bigger step size
- Resting versus exercising – randomly allocate to resting or exercising
- Memorising different word types – randomly allocate students to one of two groups with different types of words. Give them 1 minute to memorise the words. Do something else for 10 minutes and then get students to recall their words. (Put the words in a vertical list on paper.)
- Group 1 words: cat, house, boat, plate, book, cloud, Jim, hat, table, telephone, pencil, scissors, ball, ruler, door
- Group 2 words: although, however, from, such, thereby, generally, would, sufficient, never, than, already, this, of, where, also
- Standing long jumps. Randomly allocate students to one of two groups, those who jump with a target line and those who don’t have a target line. Compare the distances jumped by the two groups.
- Estimating the mid-point of a line. Measure the distance between the estimate and the mid-point. Randomly allocate participants to one of the two different types of lines.
- Vertical versus horizontal.
- One shorter line versus longer line.
Paired comparisons
- Time to stand on one leg with both eyes shut versus both open. Participants to do both and compare the differences in time standing on one leg between eyes open and eyes shut.
- Estimating the mid-point of a line. Measure the distance between the estimate and the mid-point. Participants to do both and find the difference.
- Vertical versus horizontal.
- One shorter line versus longer line.
Franklin, C., Kader, G., Mewborn, D., Moreno, J., Peck, R., Perry, M., et al. (2005). Guidelines for assessment and instruction in statistics education (GAISE) report: A pre-K-12 curriculum framework. Alexandria, VA: American Statistical Association.
Last updated September 23, 2020
TOP



