Activity: Tell me how risky
AOs |
Indicators |
Outcomes |
Snapshot
Learning experiences |
Assessment |
Spotlight
Purpose
Students demystify risk statements and conditional probabilities in order to communicate them clearly.
Achievement objectives
S 8-4 Investigate situations that involve elements of chance:
- A – calculating probabilities of independent, combined, and conditional events
Indicators
A. Calculating probabilities of independent, combined, and conditional events:
Students learn that some situations involving chance produce discrete numerical variables, that situations involving real data from statistical investigations can be investigated from a probabilistic perspective. These have probability distributions. They can be investigated by making assumptions about the situation and applying probability rules and/or by doing repeated trials of the situation and collecting frequencies.
- Selects and uses appropriate methods to investigate probability situations including
experiments,
simulations, and theoretical probability, distinguishing between deterministic and probabilistic models.
- Interprets results of probability investigations, demonstrating understanding of the relationship between true probability (unknown and unique to the situation), model estimates (theoretical probability), and experimental estimates.
- Selects and uses appropriate tools to solve problems in probability, including
two-way tables, Venn diagrams, and
tree diagrams, including
combined events.
- Solves probability problems involving
conditional probabilities, randomness,
independence, and
mutually exclusive events.
Specific learning outcomes
Students will be able to:
Diagnostic snapshot(s)
Give students a media article that discusses risk and ask them to interpret the risks mentioned, for example, from
The NZ Herald: Provincial roads hold a deadly record for risk. Stats Chat has a discussion of this article -
Proper use of denominators.
TOP
Planned learning experiences
Tell me how risky
Examples of teacher resources:
The big idea behind this activity is students can learn to interpret and communicate risk to their peers. As it discusses breast cancer, teachers need to be sensitive in case any students have family or friends with this disease. Help from the Guidance Counsellor is recommended.
Three formats of presentation
In pairs, randomly allocate one third of pairs Probability Format, one third Frequency Format and one third Pictorial Format. Ask each group to solve the problem, and present their solution to the class (on sheet of newsprint, on a mini whiteboard, as a slide presentation…).
Then show the class each problem is the same and collect their ideas about features that made each format challenging to interpret or not. Use resources such as those above and ask students to synthesise them to build their own background knowledge before they are asked to communicate another risk statement, which could be given by the teacher or taken from a recent media article.
Probability format
The probability a woman at age 50 who participates in a routine screening actually has breast cancer 0.01 (1%).
If a woman has breast cancer, the probability she will get a positive test result in a routine screening is 0.80 (80%).
If a woman does not have breast cancer, the probability she will also get a positive test result in a routine screening is 0.096 (9.6%).
A woman in this age group has a positive test result for breast cancer in a routine screening. What is the probability she genuinely has breast cancer?
Frequency format
10 of every 1000 women aged 50 who participate in routine screening actually have breast cancer.
8 of every 10 women with breast cancer will get a positive test result in a routine screening.
95 of 990 women who do not have breast cancer will also get a positive test result in a routine screening.
In a representative sample of women aged 50 who got a positive result in a routine screening, how many will you expect to genuinely have breast cancer? Express your answer as number out of number.
Now express your answer as a probability.
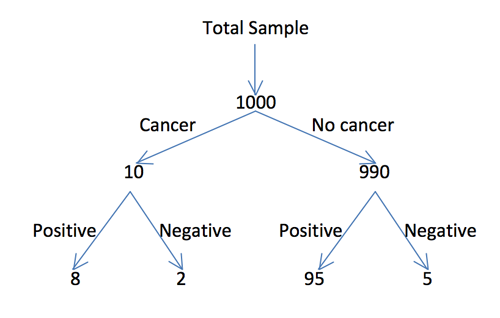
Pictorial format
The diagram below presents frequencies for a representative sample of 1000 women aged 50 who are given a routine screening for breast cancer. Cancer and No Cancer refer to the presence or absence of the disease. Positive and Negative refer to positive and negative test results during routine screening.
In a representative sample of women aged 50 who got a positive result in a routine screening, how many will you expect to genuinely have breast cancer? Express your answer as number out of number.
Now express your answer as either a probability or as a percentage.
Possible adaptations to the activity
- Another context could be used, though as risk is most commonly used for medical conditions, another medical context could be found.
TOP
Planned assessment
This teaching and learning activity could lead towards assessment in the following achievement standards:
Spotlight on
Pedagogy
Planning for effective learning
Planning should involve:
- using learning materials to focus student attention on key concepts.
Creating a supportive learning environment
In a supportive learning environment the teacher is:
- being aware of literacy implications of mathematical and statistical tasks
- expecting all students to be able to do mathematics and statistics with understanding.
Encouraging reflective thought and action
Examples of teacher actions that encourage reflective thought and action for students:
- Supporting students to explain and articulate their thinking.
Key questions that teachers can use:
- What conclusions can you draw from…?
Key competencies
Using language, symbols and texts
- Students use statistical language to communicate findings.
- Students interpret and communicate mathematical and statistical information and ideas; they know and use specialised vocabulary, as well as their own language, to explain ideas.
Participating and contributing
- Students work co-operatively as effective members of a group.
Values
- Students will be encouraged to value:
- innovation, inquiry, and curiosity, by thinking critically, creatively, and reflectively
- ecological sustainability, which includes care for the environment.
Māori/Pasifika
- Cooperative learning and creating knowledge together.
Planning for content and language learning
Last updated May 26, 2021
TOP


