Fractals activity 1: Koch curve

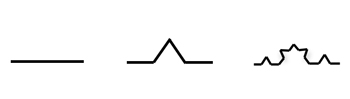
Koch Curve

Background

Fractals are interesting objects involving many sequences and series. We are focussing on the Koch curve and in particular the length of such a curve and the area under it.

Length

Above are the first three stages of the Koch curve. We start at stage 0 with a line of length 1. In the first stage the line has been divided into thirds and an equilateral triangle has been added. There are now four line segments, each of length 1/3. Each iteration adds a new collection of line segments with known lengths.

Area under the curve

This is the area between the curve and the initial line segment at stage 0. At stage one we have an equilateral triangle with a certain area, say A. We can then find out the area under the curve in terms of A.

(Teacher note: To make this task easier, a value can be assigned to the initial area.)

Task

Fill in the table and continue to answer the questions below about different features of the fractal.

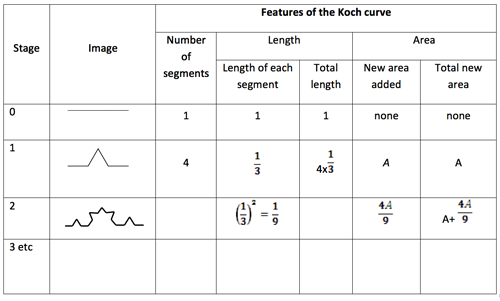
Table_features of the Koch curve

Discussion

What patterns do you notice for the number of segments, length of each segment, and total length of each segment?
(Note: This involves two features; number of segments and length of the curve).
What patterns do you notice for the area added and the new total area each stage?
(Note: This is the only place where summing the terms makes sense for the context, and involves just one feature, area.)
Investigate three different sequences or series over at least two features of the fractal. (You must include at least one sequence and one series.)
Describe how these features can be modelled using arithmetic or geometric sequences and series.
Find at least the first four terms and general term for the nth stage of your chosen features. This should include at least one partial sum.
Describe what will happen to the sequences and series as the number of iterations increase. (You may wish to use a sum to infinity where appropriate.)
Find the number of iterations or the stage at which you can guarantee the total length of the Koch curve is more than 50. (This is so you can demonstrate “finding the number of terms in a sequence”; 60 or 82.5 etc could also have been selected.)
Find the number of iterations or the stage at which you can guarantee the total area of the Koch curve is more than 1.5A. Why was 1.5A chosen and not say 10A? (Refer to your result for the sum to infinity in Q6.The value that you select must be between A and 9/5A.)
If you chose a feature other than the total length or area, then choose a limit that your chosen feature could reach. For this limit, find the number of iterations or the stage at which your feature first reaches this limit.