Activity: Fooling the teacher
AOs |
Indicators |
Outcomes |
Learning experiences |
Spotlight
Achievement objectives
S8-4 Investigate situations that involve elements of chance:
- A – calculating probabilities of independent, combined, and conditional events
Indicators
A. Calculating probabilities of independent, combined, and conditional events:
Students learn that some situations involving chance produce discrete numerical variables, that situations involving real data from statistical investigations can be investigated from a probabilistic perspective. These have probability distributions. They can be investigated by making assumptions about the situation and applying probability rules and/or by doing repeated trials of the situation and collecting frequencies.
- Selects and uses appropriate methods to investigate probability situations including
experiments,
simulations, and theoretical probability, distinguishing between deterministic and probabilistic models.
- Interprets results of probability investigations, demonstrating understanding of the relationship between true probability (unknown and unique to the situation), model estimates (theoretical probability), and experimental estimates.
- Selects and uses appropriate tools to solve problems in probability, including
two-way tables, Venn diagrams, and
tree diagrams, including
combined events.
- Solves probability problems involving
conditional probabilities, randomness,
independence, and
mutually exclusive events.
Specific learning outcomes
Students will be able to:
- recognise and describe features of random outcomes.
TOP
Planned learning experiences
Fooling the teacher
Fooling the teacher is a learning activity to encourage students to understand what randomness looks like. Randomness is a fundamental concept underlying the understanding of probability at all levels of the curriculum, from level 2 (Investigate simple situations that involve elements of chance … acknowledging uncertainty) to level 8 (Investigate situations that involve elements of chance … interpreting random variables). Understanding the nature of randomness is crucial to understanding patterns in real life situations such as coincidence, road fatalities during a public holiday weekend and gambling games.
In this activity we look at sequences of heads and tails from tossing a fair coin 50 times under the assumption that every toss is independent of all preceding ones, that is, it is a memory-less process. Students often do not appreciate that a randomly generated process can produce quite long runs of the same outcome. This results in students thinking that there is a cause or pattern in the data. A perceived pattern in data should always make students think again that what they see may be just due to random variation.
This activity has worked well with classes from year 9 to year 13, and tends to have the most impact on weak classes who are confronting their misconceptions for the first time.
Resources
- small rectangles of paper (about 5 by 10 cm), two per student
- pen or pencil each
- one coin per student
Procedure
- Give students the pieces of paper and tell them to write “fake” on one piece of paper and “real” on the other. Talk about coin tosses and establish that students know that heads and tails are equally likely and can be represented by H and T. Demonstrate tossing a coin.
- Tell students to take the piece of paper labelled “fake” and put the word side down so that they will be writing on the blank side. Draw a rectangle on the board to indicate the paper should be in landscape orientation and write a few results such as HTH in the rectangle on the board. Tell the students that they are going to try to fool the teacher by writing a string of 50 heads and tails, making it look as much like 50 real tosses as possible (some classes may be motivated by the promise of a small reward if they succeed in fooling the teacher).
- Once students have done their fake series, give out the coins and get students to do 50 actual tosses, recording the results on the blank side of the “real” paper in the same way they recorded the fake series.
- As the students finish, go to their desks, retrieve the coin, and identify which is the real series of coin tosses, checking on the back of the paper after you make your guess, and rewarding where appropriate. Encourage the students to decide if they can see any statistical difference between their fake series and their real series. Keep a record of the number of students who fool you, and the number you can guess. Students can also move around and guess other students work, checking if they got it right.
- Now ask students to take another look at their real and fake series and see if they can identify what difference you were using to make your choice. Graphing a series of real and a series of fake data may help. Discuss.
- Ask each student what the longest run was in their real data, and draw a dot plot of the longest runs on the white board. Discuss sample size, and why you wouldn’t expect 10 heads in 10 tosses, but you might get a run of 10 in 30 × 50 = 1500 tosses.
-
With a data projector, you can show the Numb3rs clip on what randomness looks like (Season 3, Traffic) or use an Excel simulation to show randomness in two dimensions:
Discussion can also be extended to real world examples like numbers of workplace accidents in one week. This exercise also leads on to consideration of how much randomness can be expected when tossing a coin or rolling a die, and how you can tell if a die or coin is weighted (but that is another lesson).
Notes for teachers
How to spot the real sequence of coin tosses
Most naïve students of probability think of randomness as being smooth and evenly spread. They include runs of 3 or 4 in their fake records, but rarely longer runs than that. To spot the real record of coin tosses, look for the longest run of heads or tails, including runs that start on one line and continue on the next. If the longest run is the same in both, look at how many times that length of run occurs and how many slightly shorter runs there are. It is important to be consistent in following the rule, and not to be influenced by messy handwriting. Occasionally a student will create a fake sequence which is obviously fake, such as 25 heads followed by 25 tails, so use your judgement about what a random distribution is likely to look like. Students who get long runs often start to draw attention to them as they keep tossing, so you would expect to have some advance notice of an unusual real distribution. The longest run observed in a real distribution of 50 tosses was a run of 13.
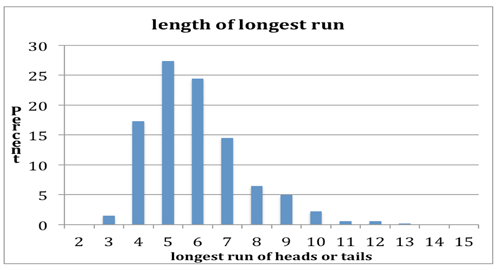
The following graph is the results of a simulation of 544 sequences of 50 coin tosses. Notice that runs of 5 or more are expected about 80% of the time, and that a run of 10 or longer is expected about 3.5% of the time, about once in a class of 28 students.
Probability theory
A run of 10 heads has a probability of 0.5^9, and there are 40 starting points in 50 tosses. So, in one series you’d expect 5/64, or 1 in 12 series.
A run of n heads in 50 tosses has an expected no. of 0.5^(n-1) x (50-n) . This function can be calculated and graphed for n = 1, 2, 3 ,4 .....
- Discuss with class: What other criteria could be used to judge whether a sequence of heads and tails was random or not? For example, other criteria could be frequency of H/T and number of runs. What would be acceptable ranges of values for these criteria when tossing a coin 50 times? Check out with simulations.
TOP
Spotlight on
Pedagogy
Enhancing the relevance of new learning
Examples of teacher actions that enhance the relevance of new learning:
- providing appropriate levels of challenge
- encouraging students to explain their thinking
- providing real-life problems in which the context is relevant to the student.
Providing sufficient opportunities to learn
Examples of teacher actions that provide sufficient opportunities to learn:
- using an engaging starting point for learning
- wrapping up the lesson or topic.
Key competencies
Thinking
- Students design investigations, explore and use patterns and relationships in data and they predict and envision outcomes.
- Students deal with uncertainty and variation, they seek patterns and generalisations.
Participating and contributing
- Students work co-operatively as effective members of a group.
- Students contribute to a culture of inquiry and learning. They share strategies and thinking and they empower and enable others.
Values
- Students will be encouraged to value:
- innovation, inquiry, and curiosity, by thinking critically, creatively, and reflectively
- ecological sustainability, which includes care for the environment.
Māori/Pasifika
Planning for content and language learning
ESOL Online -
The ESOL Principles
Last updated September 10, 2018
TOP


