Activity: Skid marks
Purpose |
AOs |
Indicators |
Outcomes |
Snapshot |
Learning experiences
Cross curricular |
Assessment |
Spotlight |
Links
Purpose
Within the context of vehicle stopping distances, students will:
- explore functions using tables, graphs, and algebra
- compare average speed and instantaneous speed.
Achievement objectives
In a range of meaningful contexts, students will be engaged in thinking mathematically and statistically. They will solve problems and model situations that require them to:
- M7-2 Display the graphs of linear and non-linear functions and connect the structure of the functions with their graphs.
- M7-6 Manipulate rational, exponential, and logarithmic algebraic expressions.
- M7-7 Form and use linear, quadratic, and simple trigonometric equations.
- M7-8 Form and use pairs of simultaneous equations, one of which may be non-linear.
TOP
Indicators
- Makes connections between representations, such as f(x) notation, tables, mapping, equations, wordss and graphs.
- Identifies and uses appropriate key features, that is, symmetry, period, amplitude, intercepts, maxima, minima, asymptotes, domain, and range.
- Solves problems that involve manipulating rational, exponential, and logarithmic algebraic expressions.
- Solves problems that can be modelled by linear [or] quadratic … equations and interprets solutions in context.
- Solves problems that can be modelled by pairs of simultaneous equations where one is linear and the other equation is non-linear.
- Chooses appropriate methods and uses them to solve simultaneous equations.
- Interprets the existence and type of solution(s) in the context of the situation.
TOP
Specific learning outcomes
Students will be able to:
- model data making connections between graphs, tables, and algebraic representations
- write simultaneous equations and use them to answer questions.
TOP
Diagnostic snapshot(s)
Students need to have some understanding of families of functions and transformations.
TOP
Planned learning experiences
The teacher sets the scene by discussing traffic accidents, vehicle stopping distances, etc. From this, the class develop focus questions and investigate functions, mathematical models, etc, to answer the questions.
Information
Drivers stopping to avoid collisions need to be aware of the factors that affect the distance a car travels before coming to a complete stop.
Two critical factors affecting the total stopping distance are:
- the reaction distance – the distance travelled during the time a driver sees a hazard and the time when he or she applies the brakes
- the braking distance – the distance travelled from the moment the brakes are applied until the car stops.
Both of these distances depend on the speed of the car at the time the driver sees the hazard.
The Ministry of Transport has obtained data for a 45 year-old male driving a car at different speeds.
| S – Speed (km/h)
| 10
| 20
| 30
| 40
| 50
| 60
| 70
| 80
| 90
| 100
|
| R – Reaction distance (m)
| 2
| 4
| 6
| 8
| 10
| 12
| 14
| 16
| 18
| 20
|
| B – Braking distance (m)
| 2
| 3
| 6
| 10
| 15
| 22
| 29
| 38
| 48
| 60
|
Focus questions
- What is the relationship between vehicle breaking distance, reaction distance, and speed?
- If we know the length of the skid marks, how can we work out the speed a vehicle was going?
Anticipated learning outcomes
Students find mathematical models for vehicle breaking distance and reaction distance as a function of speed and use these to solve problems.
Possible student response
We used mathematical models to investigate the relationship between speed, reaction distance, and braking distance.
The length of the skid mark is the breaking distance. We used technology to find the line of best fit. This is modelled by f(x) = 0.0062x2-0.0445x + 1.6833 where x is speed in kph.
The reaction distance is the distance travelled in the time between when the driver starts to react and when they put the brakes on.
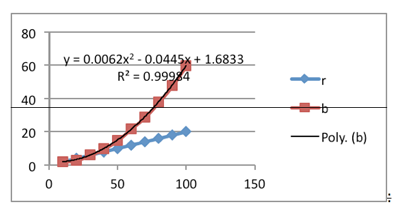
Driver breaking distance
For a car travelling at 30kph, the reaction distance and breaking distance are the same. So total stopping distance is double reaction distance at 30kph.
Below 30kph, the reaction distance is greater than the length of the skid marks.
If we can measure the reaction distance, we can calculate the speed the car was travelling by using f-1(x).
Possible adaptations to the activity
Questions can be driven by individual students, who could write questions based on the data provided, and then carry out a mathematical investigation in order to answer their own question. They could present their answer as a report to the class.
Students could also use the web to find other data from which they can create models, which they then use to answer questions, for example, around alcohol and drug absorption, projectile motion, etc.
Other possible questions and learning outcomes
- How does average speed compare with instantaneous speed? (Anticipated learning outcome: Students show understanding of the derivative as a measure of rate of change at a point.)
- Can we use mathematics to predict the value of a car over time? (Anticipated learning outcome: Students fit exponential function(s) to depreciation data.)
TOP
Cross-curricular links
- Science, for example, kinematics.
Extension/enrichment ideas
RISP activities:
- Risp 6: The gold and silver cuboid
- Risp 7: The two special cubes
- Risp 12: Two repeats
- Risp 16: Never positive
- Risp 17: Six parabolas
TOP
Planned assessment
This teaching and learning activity could lead towards assessment in the following achievement standards:
TOP
Spotlight on
Pedagogy
- Planning for effective learning by:
- using learning materials to focus student attention on key concepts.
- Enhancing the relevance of new learning by:
- providing appropriate levels of challenge
- encouraging students to explain their thinking.
- Creating an inclusive learning environment through:
- expecting all students to be able to do mathematics and statistics with understanding.
- Encouraging reflective thought and action by:
- supporting students to explain and articulate their thinking
- engaging students in evaluating different methods and strategies.
- Enhancing the relevance of new learning through:
- encouraging students to explain their thinking
- supporting students to connect concepts and applications
- providing real-life problems in which the context is relevant to the student.
Key competencies
- Using languages, symbols, and texts:
- Using the symbols and conventions of mathematics to make connections between different representations (tables, graphs, diagrams, equations).
- Using symbols and diagrams to solve problems.
- Interpreting and communicating information and ideas, knowing and using specialised vocabulary, as well as their own language, to explain ideas.
- Interpreting word problems and visual representations.
- Thinking:
- Using mathematics to model real life and hypothetical situations; making conjectures, challenging assumptions and thinking; and engaging in sense-making.
- Asking questions, wanting to know “why”, making connections, and discerning if answers are reasonable.
- Relating to others:
- Working as a group, understanding others’ thinking, accepting and valuing differing viewpoints, negotiating meaning.
Values
Students will be encouraged to value:
- excellence, by aiming high and by persevering in the face of difficulties
- innovation, inquiry, and curiosity, by thinking critically, creatively, and reflectively.
Māori/Pasifika
Planning for content and language learning
TOP
Links
Last updated September 9, 2018
TOP


