Activity: Fair spinners
AOs |
Indicators |
Outcomes |
Snapshot |
Learning experiences
Extension ideas |
Assessment |
Spotlight |
Links
Purpose
Use simple spinners to:
- estimate mean and standard deviation of a discrete random variable
- develop a model for a discrete random variable
- build a justified model for the sum of two spins of a given spinner.
Achievement objectives
S8-4 Investigate situations that involve elements of chance:
- B – calculating and interpreting expected values and standard deviations of discrete random variables
Indicators
B. Calculating and interpreting expected values and standard deviations of discrete random variables:
- A statistical data set may contain discrete numerical variables Makes a reasonable estimate of mean and standard deviation from a plot of the distribution of a
discrete random variable.
- Solves and interprets solutions of problems involving calculation of mean, variance and standard deviation from a
discrete probability distribution.
- Solves and interprets solutions of problems involving linear transformations and sums (and differences) of
discrete random variables.
These have
frequency distributions that can be converted to empirical probability distributions. Distributions from both experiment and theory have the same set of possible features (centre, spread, clusters, shape, tails, and so on) and the same measures (mean, SD, and so on) can be calculated for them.
Specific learning outcomes
Students will be able to:
- make a reasonable estimate of mean and standard deviation from a plot of the distribution of a
discrete random variable
- select and use an appropriate distribution to solve a problem, demonstrating understanding of the relationship between true probability (unknown and unique to the situation), model estimates (theoretical probability) and experimental estimates
- solve and interpret solutions of problems involving linear transformations and sums (and differences) of
discrete random variables
- solve and interpret solutions of problems involving calculation of mean, variance and standard deviation from a
discrete probability distribution.
TOP
Diagnostic snapshot(s)
Revisit mean and standard deviation, sketch distributions with labelled axes to show effect of changing parameters.
Planned learning experiences
Estimating mean and standard deviation from a plot
The starting point should be an understanding of the mean as a balance point for a distribution. Link this to childhood experience of playing on a see-saw. Finding the balance point can be modelled with a flat wooden ruler on a wooden cuboid (the balance point) and multi-link cubes (the data). As the data values change, (the positions of the cubes change), the position of the cuboid (the balance point) has to change for the ruler to be level. A variety of distributions should be investigated along with the effect of extreme values.
This
YouTube applet can be used to show physically how to find the mean as the balance point of a discrete distribution. It shows simple situations where the mean is a member of the data set. Teachers will need to adapt it for distributions where the mean is not a member of the data set, which could be done as an investigation by students.
Once an understanding of mean as balance point is established, estimating the mean from a discrete distribution can be based on estimating the median and then adjusting the estimate according to the shape of the distribution; the mean is pulled towards extreme values and the balance point is not the median if the distribution is skewed.
Estimating the standard deviation should be built on an understanding of the standard deviation as a measure of the average deviation from the mean and its being stretched by extreme values. For data that is approximately normal, the standard deviation is roughly 1/6 of the range. If the distribution is skewed the initial estimate should be adjusted (stretched). Based on both the definition of an outlier as being 4 standard deviations from the mean and Tukey’s classification of an outlier as being 1.5 x IQR above or below the quartiles, when data is not approximately normally distributed, standard deviation can be approximated by the semi-IQR (half the IQR). If students see lots of distributions with the means and standard deviations shown on them, they should get a good idea of how to estimate both.
Probability: Fair spinners
Imagine you spin this spinner once and record the number, then spin it again and add the second number to the first.
Spinners are made of card, and a paperclip is flicked round a pen positioned at the centre of the circle.
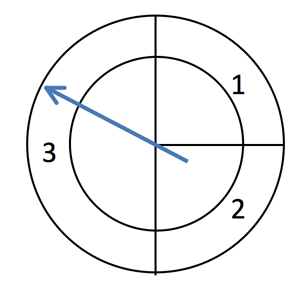
First students are to record their hunch about a possible distribution for the totals they will get when the spinner is spun twice, taking into account the least, greatest, most likely and least likely totals. A rough sketch of the shape of the distribution is all that is expected. (Rationale: spinner does not show equally likely outcomes to avoid limitations and possible misconceptions. Expect students to be surprised as it is unlikely their hunches will be correct.)
Collect data (number of trials to be decided by students), sketch the experimental distributions and describe the experimental distributions in terms of mean and standard deviation. Class data could be combined to create one distribution for discussion. It is important that students do not calculate mean and standard deviation, but estimate them, as this is a first step in building a model.
Discuss what is the same and what is different about the hunches and the data. What have the students learned about the distribution from the experiment?
In cooperative groups, students now build a probability model (theoretical distribution) for adding the outcomes of 2 spins of this spinner, taking into account such factors as the underlying theoretical model for each spinner and the random (or predictable) nature of spinning. Assumptions in the model should be identified and justified in context. Students explain the reason that neither model probabilities nor experimental probabilities are the (unknown) true probabilities. Students should use their model to make predictions and discuss the reliability of their predictions.
Students could systematically write down all possible outcomes, by using a tree diagram, a 2 way table or graph (ie a histogram) with probabilities in vertical dimension, and sum along diagonals. This gives the probabilities for the distribution of the sum.
Extension: Investigate other spinners and possible models for sums, differences, products of 2 (or more) spins. Build models for these new situations and use them to show understanding of estimated means and standard deviations for comparing the 2 distributions.
Linear transformations and sums and differences of discrete random variables
Spinners can be used to investigate the effects of linear transformations (and sums and differences) of discrete random variables by working with theoretical probability models already established. A guided and full investigation should lead to the students discovering the transformation rules for means and variance for themselves.
Such investigations provide opportunities to directly address misconceptions about adding standard deviations and about doubling the value of a random variable being the same as adding two occurrences of the same random variable.
Possible adaptations to the activity
- Spinners could be used for learning to use tables and tree diagrams to solve probability problems.
TOP
Extension/enrichment ideas
What if numbers are multiplied, subtracted? What if two different (dissimilar spinners) are added? Could the number of sectors on a spinner be related to the parameters of the distribution of totals?
Planned assessment
This teaching and learning activity could lead towards assessment in the following achievement standards:
Spotlight on
Pedagogy
Planning for effective learning
Planning should involve:
- starting with familiar contexts, concrete materials and prior knowledge, and moving to generalisations and abstract ideas (and back and forth between these as needed).
Encouraging reflective thought and action
Examples of teacher actions that encourage reflective thought and action for students:
- supporting students to explain and articulate their thinking
- encouraging students to fine-tune their statistical thinking.
Key questions that teachers can use:
- What do you notice?
- What does this make you wonder?
- What conclusions can you draw from…?
Key competencies
Relating to others
- Students share their ideas, accept a range of approaches and respect others’ thinking.
- Students work collaboratively and cooperatively, taking on a range of roles. They think, share ideas in pairs, and share ideas in groups of four.
Participating and contributing
- Students work co-operatively as effective members of a group.
- Students contribute to a culture of inquiry and learning. They share strategies and thinking and they empower and enable others.
Values
- Students will be encouraged to value:
- innovation, inquiry, and curiosity, by thinking critically, creatively, and reflectively
- ecological sustainability, which includes care for the environment.
Māori/Pasifika
- Cooperative learning and creating knowledge together.
- Appreciate the changing nature of tangata whenua.
Planning for content and language learning
Links
Last updated September 10, 2018
TOP


