Glossary page D
Data
A term with several meanings.
Data can mean a collection of facts, numbers, or information; the individual values of which are often the results of an experiment or observations.
If the data are in the form of a table with the columns consisting of variables and the rows consisting of values of each variable for different individuals or values of each variable at different times, then data has the same meaning as data set.
Data can also mean the values of one or more variables from a data set.
Data can also mean a variable or some variables from a data set.
Properly, data is the plural of datum, where a datum is any result. In everyday usage, the term data is often used in the singular.
See: data set
Curriculum achievement objectives references
Statistical investigation: All levels
Statistical literacy: Levels 2, (3), (4), 5, (6), (7), (8)
Data display
A representation, usually as a table or graph, used to explore, summarise, and communicate features of data.
Data displays listed in this glossary are: bar graph, box and whisker plot, dot plot, frequency table, histogram, line graph, one-way table, picture graph, pie graph, scatter plot, stem-and-leaf plot, strip graph, tally chart, two-way table.
Curriculum achievement objectives references
Statistical investigation: Levels 1, 2, 3, 4, 5, 6, (7), (8)
Statistical literacy: Levels 2, 3, (4), (5), 6
Data set
A table of numbers, words or symbols, the values of which are often the results of an experiment or observations. Data sets almost always have several variables.
Usually the columns of the table consist of variables and the rows consist of values of each variable for individuals or values of each variable at different times.
Example 1 (Values for individuals)
The table below shows part of a data set resulting from answers to an online questionnaire from 727 students enrolled in an introductory statistics course at the University of Auckland.
Online questionnaire answers data set.
| 1
| female
| Jan
| 1984
| Other European
| 2
| 3
| 55
| 50
|
| 2
| female
| Nov
| 1990
| Chinese
| 15
| 11
| 53
| 49
|
| 3
| male
| Jan
| 1990
| NZ European
| 18
| 2
| 68
| 60
|
| . . .
| . . .
| . . .
| . . .
| . . .
| . . .
| . . .
| . . .
| . . .
|
Example 2 (Values at different times)
The table below shows part of a data set resulting from observations at a weather station in Rolleston, Canterbury, for each day in November 2008.
Time series weather observations data set.
| 1
| 26.8
| 0.5
| 1015.1
| 70.3
|
| 2
| 19.7
| 0.0
| 1015.6
| 38.9
|
| 3
| 19.5
| 0.0
| 1011.1
| 29.6
|
| . . .
| . . .
| . . .
| . . .
| . . .
|
Alternative: dataset
Curriculum achievement objectives references
Statistical investigation: Levels 3, (4), 5, (6), 7, 8
Dependent variable
A common alternative term for the response variable in bivariate data.
Alternatives: outcome variable, output variable, response variable
Curriculum achievement objectives reference
Statistical investigation: (Level 8)
Descriptive statistics
Numbers calculated from a data set to summarise the data set and to aid comparisons within and among variables in the data set.
Alternatives: numerical summary, summary statistics
Curriculum achievement objectives references
Statistical investigation: Levels (5), (6), (7), (8)
Desk review
A review of a questionnaire for the purpose of finding likely problems with it before it is used in a survey.
Ideally, a desk review should be carried out by at least two people, including someone who did not design the questions. It should be carried out before a pilot survey and done at several stages throughout a survey, especially after any changes have been made.
A desk review should check the questionnaire:
- is consistent with the survey objectives
- uses consistent terms and language
- uses language appropriate for the intended respondents
- uses questions that are reasonably simple, unambiguous and unbiased
- is designed to be easy to follow.
Alternative: desk evaluation
Curriculum achievement objectives reference
Statistical investigation: (Level 7)
Deterministic model
A model that will always produce the same result for a given set of input values. A deterministic model does not include elements of randomness. A model, being an idealised description of a situation, is developed by making some assumptions about that situation.
A deterministic model will often be written in the form of a mathematical function.
Example
A model for calculating the amount of money in a term deposit account after a given time will always produce the same answer for a given initial deposit, interest rate and method of calculating the interest.
If the initial deposit is P dollars, the interest rate is r% per annum but the interest is calculated daily, then the amount in the account, in dollars, after n days can be calculated by
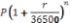 . For given values of P, r and n the result of the calculation of
. For given values of P, r and n the result of the calculation of
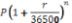 will be the same. This model assumes that the interest rate remains constant, no money is withdrawn from the account and that no further money is deposited into the account.
will be the same. This model assumes that the interest rate remains constant, no money is withdrawn from the account and that no further money is deposited into the account.
See: probabilistic model
Curriculum achievement objectives reference
Probability: (Level 8)
Discrete distribution
The variation in the values of a variable that can only take on distinct values, usually whole numbers.
A discrete distribution could be an experimental distribution, a sample distribution, a population distribution, or a theoretical probability distribution.
Example 1
At Level 8, the binomial distribution is an example of a discrete theoretical probability distribution.
Example 2
Consider a random sample of households in New Zealand. The distribution of household sizes from this sample is an example of a discrete sample distribution.
See: distribution
Curriculum achievement objectives references
Statistical investigation: Levels (5), (6), (7), (8)
Probability: Levels 5, 6, 7, (8)
Discrete random variable
A random variable that can take only distinct values, usually whole numbers.
Example
The number of left-handed people in a random selection of 10 individuals from a population is a discrete random variable. The distinct values of the random variable are 0, 1, 2, … , 10.
Curriculum achievement objectives reference
Probability: Level 8
Discrete situations
Situations involving elements of chance in which the outcomes can take only distinct values.
If the outcomes are categories, then this is a discrete situation. If the outcomes are numerical, then the distinct values are often whole numbers.
Curriculum achievement objectives reference
Probability: Level 6
Disjoint events
Alternative: mutually exclusive events
Curriculum achievement objectives reference
Probability: (Level 8)
Distribution
The variation in the values of a variable. The collection of values forms an entity in itself; a distribution. This entity (or distribution) has its own features or properties.
The type of distribution can be described in several different ways, including:
- the type of variable (for example, continuous distribution, discrete distribution),
- the way the values were obtained (for example, experimental distribution, population distribution, sample distribution), or
- the way the occurrence of the values is summarised (for example, frequency distribution, probability distribution).
Other types of distributions described in this glossary are bootstrap distribution, re-randomisation distribution, sampling distribution and theoretical probability distribution.
See: bootstrap distribution, continuous distribution, discrete distribution, experimental distribution, features (of distributions), frequency distribution, population distribution, probability distribution, re-randomisation distribution, sample distribution, sampling distribution, theoretical probability distribution
Curriculum achievement objectives references
Statistical investigation: Levels 4, 5, 6, (7), (8)
Probability: Levels 4, 5, 6, 7, 8
Dot plot
A graph for displaying the distribution of a numerical variable in which each dot represents a value of the variable.
For a whole-number variable, if a value occurs more than once, the dots are placed one above the other so that the height of the column of dots represents the frequency for that value.
Dot plots are particularly useful for comparing the distribution of a numerical variable for two or more categories of a category variable; this is shown by displaying side-by-side dot plots on the same scale. Dot plots are particularly useful when the number of values to be plotted is relatively small.
Dot plots are usually drawn horizontally, but may be drawn vertically.
Example
The actual weights of random samples of 50 male and 50 female students enrolled in an introductory statistics course at the University of Auckland are displayed on the dot plot below.
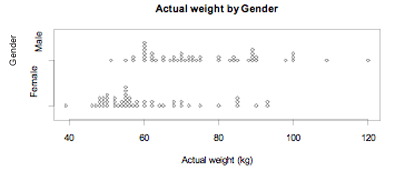
If you cannot view or read this diagram/graph, select this link to
open a text version
Alternative: dot graph, dotplot
Curriculum achievement objectives references
Statistical investigation: Levels (3), (4), (5), (6), (7), (8)
Last updated October 9, 2013
TOP


