Activity: Linking integration and differentiation
AOs |
Indicators |
Outcomes |
Snapshot |
Learning experiences |
Cross curricular |
Extension ideas |
Assessment |
Spotlight |
Links |
Connections
Purpose
Use a numerical approach to solve problems involving summation so solve integration problems. Define integration as the process of solving a problem by cutting it into small problems of the same type, solving the smaller problems (at least approximately) and summing the answers to get solution of original problem. An integration problem is a problem that can be solved using this method. One example of an integration problem is the problem of finding the area under a curve. The integral is the area under curve. Introduce notation for this.
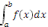 is area under f(x) between x=a and x=b and emphasise the need for a shortcut to solve these problems.
is area under f(x) between x=a and x=b and emphasise the need for a shortcut to solve these problems.
Take a detour to find velocity from displacement and develop understanding of differentiation from this. Use a numerical approach to solve problems involving finding rates of change. Find a shortcut for finding the derivative. Develop ideas around fundamental theorem of calculus and make the link to see integration and differentiation as inverse processes. Rate of change of an area under the function is the height of function. Area is anti-derivative of the function. (The fundamental theorem of calculus, including: if f is continuous on [a, b] and F(x) =
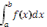 for [a, b] then F' = f (explores using technology) and if F' = f then
for [a, b] then F' = f (explores using technology) and if F' = f then
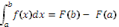 ).
).
Having made connection between integration and anti-differentiation, revisit integration problems and solve using anti-differentiation methods.
TOP
Achievement objectives
- M 8-2 Display and interpret the graphs of functions with the graphs of their inverse and/or reciprocal functions.
- M 8-10 Identify discontinuities and limits of functions.
- M 8-11 Choose and apply a variety of differentiation, integration, and anti-differentiation techniques to functions and relations, using both analytical and numerical methods.
TOP
Indicators
Understands and uses a range of differentiation techniques including:
- first principles (only for polynomials of degree ≤ 3)
- product rule, quotient rule, chain rule
- other techniques including implicit or parametric differentiation (for conic relations)
- connecting derivative and instantaneous rate of change.
Functions include polynomials, ex, ln(x), trig functions, xn, n ∈ R .
Develops an understanding of integration by:
- using numerical methods for finding areas under curves (rectangle rule, trapezium rule)
- relating the definite integral to the limit of a sum (Riemann Integral)
- linking integration and anti-differentiation using the fundamental theorem of calculus, including:
- Part 1: If f is continuous on [a, b] and F(x) =
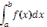 for [a, b] then F' = f (explores using technology) (Note: this guarantees that an anti-derivative does exist for Part 2.)
for [a, b] then F' = f (explores using technology) (Note: this guarantees that an anti-derivative does exist for Part 2.)
- Part 2: If F' = f then
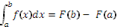 .
.
Uses a variety of integration techniques for functions including polynomials, xn ( n ∈ R), ex, sin(x), cos(x), f ' ( g ( x ) ) ( g ' ( x ) ) ,
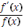 .
.
Applications include:
- finding areas under and between curves
- rates of change
- kinematics.
TOP
Specific learning outcomes
Students will be able to:
- develop an understanding of integration by:
- using numerical methods for finding areas under curves (rectangle rule, trapezium rule)
- relating the definite integral to the limit of a sum (Riemann Integral)
- linking integration and anti-differentiation using the fundamental theorem of calculus
- understand and use a range of differentiation techniques including:
- first principles (only for polynomials of degree ≤ 3)
- product rule, quotient rule, chain rule
- other techniques including implicit or parametric
- differentiation (for conic relations)
- connecting derivative and instantaneous rate of change
- solve applications include:
- finding areas under and between curves
- rates of change
- kinematics.
TOP
Diagnostic snapshot(s)
Students need an understanding of level 7 families of functions and graphs and algebra.
TOP
Planned learning experiences
Provide data which requires the need to estimate area using integration in context. For example, finding distance travelled given speed over time.
Initial focus is on distance, speed and time; Use the fact that distance travelled is rate multiplied by time to find distance from speed and time.
Progression
Find the total distance travelled from velocity and time given:
- Velocity/time data
- Graph of velocity and time
- Velocity as function of time (simple parabolic). Find upper and lower limits. Explore various sub-intervals.
- Velocity in terms of linear piecewise function. Check area under graph does give distance covered.
Encourage students to realise that using rectangles is simpler to use. To estimate upper and lower bounds, students should divide area up into smaller rectangles that are either slightly above or slightly below the curve.
Explore a wide variety of problems that are solved by similar method (numerical method for finding area under curve). There are plenty of problems as traditional Simpson’s and Trapezium Rule questions.
Define integration as the process of solving a problem by cutting it into small problems of the same type, solving the smaller problems (at least approximately) and summing the answers to get a solution of the original problem. An integration problem is a problem that can be solved using this method. One example of an integration problem is the problem of finding the area under a curve. The integral is the area under curve. Introduce notation for this.
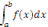 is area under f(x) between x=a and x=b.
is area under f(x) between x=a and x=b.
Lead the need for developing an alternative method for doing this. Take a detour to find velocity from displacement and develop understanding of differentiation from this. Then make the link to see integration and differentiation as inverse processes. Rate of change of an area under the function is the height of function. Area is anti-derivative of function. Revisit problems solved numerically at the start of this topic and use anti-differentiation to solve those that you can.
Example
Task 1
Mrs Brown and her husband are on a very long journey by car. They are travelling on a highway that bypasses all towns, and Mr Brown had extra fuel tanks fitted to his car to extend the range to about 1500km. Mrs Brown likes to keep track of the distance she has covered, but discovers soon after departing from home that the odometer (distance meter) in the car is broken, and Mr Brown forgot to bring the road map. The speedometer still works and Mrs Brown has a watch.
- Describe how they could determine the distance they have travelled.
- Mrs Brown decides she will record the speedometer reading from time to time, and that she will use these readings to estimate the distance covered from this record. The record for the first two hours of the journey is given below. They left home at 8:30 am. The speeds are given in km/h.
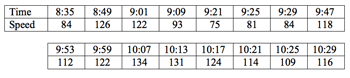
Time and speed.
Estimate the total distance travelled.
Task 2
Your task is to estimate the total distance travelled. Give an upper and lower bound for your estimate. (i.e. what is the greatest distance you estimate they have travelled? What is the least?)
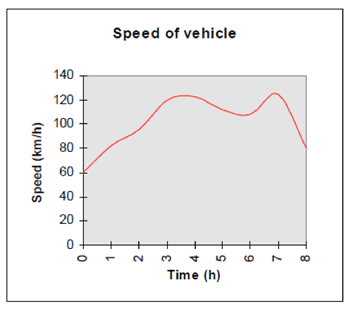
Speed of vehicle_graph
Task 3
You have moved into a new neighbourhood and are going to drive to a grocery store for the first time. You are interested in knowing the distance from your house to the store, but unfortunately your car’s odometer is broken. Fortunately, the speedometer works. With the aid of the digital camera in the cell phone and a curve-fitting program on your PC, you are able to construct a table of values of your speed during the trip to the store, and discover that during the two-minute drive to the store your speed (in metres per minute) can be modelled by the function
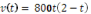 .
.
a) Graph this function.
b) How far (to the nearest 50 metres) is it from your house to the store?
c) Explore upper and lower bounds for your estimate of distance.
d) Use different sub-intervals to get as accurate an estimate of distance as possible.
Task 4
Find the total distance covered when speed is described by a piecewise function, v.
v is velocity in km/h and time is t in hours.
v = 600t; 0 ≤ t ≤ 1
v = 600; 1 < t ≤ 2
v = 1200 – 300t; 2 < t ≤ 4
Test the assumption that area under the graph is the same as the distance travelled.
Task 5
Explore wide variety of problems that are solved by similar method (numerical method for finding area under curve).
Example
A projectile is fired from ground level, and hits a target (also at ground level) 150 metres away. The maximum height it reaches during its flight is 281.25 metres.
a) Write a function which gives the height of the projectile in terms of the horizontal distance from its launch site. You can assume that the projectile travels along a parabolic path.
b) How far does the projectile travel during its flight?
Task 6
Find the velocity given information about distance and time.
Gowell's transport company has to make a delivery from Bloemfontein to Cape Town. The distance between the two cities is 1041 km. The driver sets off at 5:30am and must arrive in Cape Town before 5:00pm. Every hour that he is late the company has to pay a penalty fine. For safety reasons the company insists that the driver take 3 half-hour stops to rest and refuel if necessary. Shortly after leaving Bloemfontein he notices that his speedometer is not working. The odometer still works and the driver has a watch.
- Describe how the driver could determine when he will arrive in Cape Town.
The driver decides to record the odometer recordings from time to time, and he will use these readings to estimate his speed. After four hours the driver takes his first rest. The record for these four hours is given below.
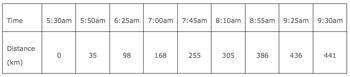
Time and distance
- Estimate, as best you can, the average speed of the vehicle during the first four hours.
- Provide a written account of how you obtained your estimate.
- If the driver managed to maintain a similar speed for the rest of the journey would he reach Cape Town before 17:00? Explain your answer.
- Due to the passes through the mountains in the Western Cape, the driver will have to reduce his average speed by 10 km/h for the last 250 km. Will the driver make it to Cape Town on time? Explain your answer.
- During the driver’s first stop he meets you in the service station and explains his problem to you. Could you help him to devise a plan that will give him a more accurate or easier to calculate estimate of his required speed? Explain your plan.
TOP
Cross curricular links
- Physics (kinematics, etc)
- Economics (maximising profit, minimising cost)
- Surveying
TOP
Extension/enrichment ideas
For algebraically strong students, ask students to do examples of calculating areas with n sub intervals and then sum these to generate a general formula. This involves the use of formulas for sums of squares and sums of cubes.
TOP
Planned assessment
This teaching and learning activity could lead towards assessment in the following achievement standards:
TOP
Spotlight on
Pedagogy
Planning for effective learning:
- Using learning materials to focus student attention on key concepts.
Creating an inclusive learning environment:
- Expecting all students to be able to do mathematics and statistics with understanding.
Encouraging reflective thought and action:
- Supporting students to explain and articulate their thinking.
- Engaging students in evaluating different methods and strategies.
- Getting students to justify, compare and contrast solutions.
- Probing student thinking.
Enhancing the relevance of new learning:
- Providing appropriate levels of challenge.
- Exploring generalisations made by students.
- Encouraging students to explain their thinking.
- Supporting students to connect concepts and applications.
- Providing real-life problems in which the context is relevant to the student.
Key competencies
Thinking:
- Students select appropriate methods and strategies when solving problems.
- Students use mathematics to model real life and hypothetical situations; they make conjectures, challenge assumptions and thinking, and they engage in sense making.
- Students ask questions, want to know ‘why’, make connections and discern if answers are reasonable.
- Students seek patterns and generalisations.
Using languages symbols and texts:
- Students use the symbols and conventions of mathematics to make connections between different representations (tables, graphs, diagrams, equations).
- Students use symbols and diagrams to solve problems.
- Students interpret and communicate information and ideas; they know and use specialised vocabulary, as well as their own language, to explain ideas.
- Students interpret word problems and visual representations.
Relating to others:
- Work as a group, understand others thinking, accept and value differing viewpoints, negotiating meaning.
Values
Students will be encouraged to value:
- excellence, by aiming high and by persevering in the face of difficulties
- innovation, inquiry, and curiosity, by thinking critically, creatively, and reflectively.
Māori/Pasifika
Planning for content and language learning
- ESOL Online -
The ESOL Principles
- Provide multiple opportunities for authentic language use with a focus on students using academic language: Is the language focus on key language?
- Do I make sure the students have many opportunities to notice and use new language?
- Reinforce vocabulary of functions, relationships and terminology of calculus.
TOP
Links
TOP
Connections
- McIntyre, R. (1994). Cooperative mathematics for level seven. Auckland, New Zealand: Longman Paul.
Last updated September 17, 2018
TOP




