Activity: Lego exercise
AOs |
Indicators |
Outcomes |
Snapshot |
Learning experiences
Assessment |
Spotlight |
Links
Purpose
- To investigate a unfamiliar situation and to establish and improve a probability model.
- To evaluate whether there is no model for the situation, or whether the model is poor or good (fit for purpose).
Achievement objectives
S 8-4 Investigate situations that involve elements of chance:
- C. Applying distributions such as the Poisson, binomial, and normal
Indicators
C. Applying distributions such as the Poisson, binomial, and normal:
They learn that some situations that satisfy certain conditions can be modelled mathematically. The model may be
Poisson,
binomial,
normal, uniform, triangular, or others, or be derived from the situation being investigated.
- Selects and uses an appropriate distribution to model a situation in order to solve a problem involving probability.
- Selects and uses an appropriate distribution to solve a problem, demonstrating understanding of the relationship between true probability (unknown and unique to the situation), model estimates (theoretical probability) and experimental estimates.
- Uses a distribution to estimate and calculate probabilities, including by
simulation.
TOP
Specific learning outcomes
Students will be able to:
- build a model for an unfamiliar probability situation and evaluate its effectiveness.
Diagnostic snapshot(s)
- Check student understanding of modelling simple situations such as using a spinner with ¼ labelled 1, ¼ labelled 2, and ½ labelled 3, spinning twice and totalling the numbers shown.
Planned learning experiences
Building a model of a discrete distribution using Lego blocks
Big ideas
- True probability, model estimate, experimental estimate
- Poor model, good model, no model
Equipment
Lego 2 by 2 bricks.
Process
Important: Do NOT give out the bricks to start with.
Teacher led activity
Look at a 2 by 2 block. How many ways can it land, if we throw it?
- Three: Studs up, studs down, and studs on the side.
Students in pairs
Estimate the probability of each of these outcomes before you start testing. Record your hunch for each of the three probabilities.
For example: This estimate is based on the idea that each side is more-or-less equally likely, but that there are four different sides that constitute being on the side.
| Position
| Studs up
| Studs down
| Studs on the side
|
| Probability
| 1/6=0.167
| 1/6=0.167
| 4/6=0.666
|
Note: This initial model is specified by the sample space (the set of possible outcomes), the probability of each outcome, and assumes a random process and independence.
In class
Collect class estimates for each probability and graph them.
Estimate the parameters (mean, SD...) of each probability distribution on the board, or in a spreadsheet.
Look at the range of parameter estimates. Make sure each distribution sums to 1.
Find the mean of the each of the responses for each outcome. This is a group subjective estimate of the mean of the probability distribution.
We can see later on if this is close to the experimental result – applying the theory of wisdom of the crowd.
What kind of model is this? It is an initial model based on very limited information and limited prior experience; based on intuitive assumptions about the behaviour of the 3 types of side. It may be a good model of the real world system or a poor model. To find out we need to experiment to see whether it is an adequate model of the real world, that is, whether our probability model fits with the data. If our initial model is inadequate, we need to modify it.
How can we test this model? By experimenting.
In pairs
Give out the Lego bricks now – preferably five or ten each with shakers – work in pairs, one shaking, and one recording.
Students now generate some experimental data: for example, 20 shakes each, and calculate their own probability distributions. With 5 bricks this gives a total 100 outcomes for each pair.
In class
Now write down the experimental probability distributions of each pair of students on the board or in a spreadsheet. Discuss the variation amongst the probability distributions.
Total up the frequencies for each outcome and plot the overall distribution (do as a frequency and probability distribution). This is akin to using the results from the whole class as one big sample.
Teacher led discussion
What kind of model is this? Model based on experimental estimates. This experimental probability distribution estimates the ‘true’ probability distribution? How does it compare with the subjective estimates we started with? You could use a graph for comparing.
Is it a good model? The answer depends on the purpose of the investigation. At the moment there is no purpose. If it were high stakes and involving human life or a large amount of money, this is unlikely to be a big enough sample and we would see this as a poor model, as it would not be fit for purpose and would require further development. If low stakes, for example, a children’s game, it is a good model inasmuch as it is good enough for the purpose.
This is the model we are going to use from now on. Look back at the original distribution of estimates. How do the two distributions, subjective estimates and experimental, compare? What is the same and what is different about the 2 distributions?
New tack – teacher led introduction
Why can’t the mean (expected value) of the distribution be calculated? The outcomes are not numeric values, but studs up, studs down, studs on the side.
Let’s turn it into a game and explore the behaviour further.
We can assign values for a random variable to each of the three outcomes of tossing the brick, which will be the amount of money awarded if that outcome occurs.
For example:
| Position
| Studs up
| Studs down
| Studs on the side
|
| Probability
| 1/6=0.167
| 1/6=0.167
| 4/6=0.666
|
| Value
| $10
| $20
| $0
|
Expected value = 0.167×10+0.167×20+0.666×0 = 5.01
Standard deviation =
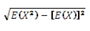 = 7.64
= 7.64
In pairs
Each pair makes up a set of values for the three outcomes that will give an expected value of 5. The numbers can be as large or small as you like, and can be negative. (This might be good to do using a spreadsheet.) Or algebraically – fix two values and re-arrange an equation to find the third. Imagine this is a game you can play: you pay $5 and you get back the amount determined by the toss of the brick.
Write the values on the board/spreadsheet.
Teacher led class discussion
Compare the distributions. Imagine they involve money and you have to pay $5 to play. Would they be fair?
Which is the highest stake? Which has the riskiest outcome? What do you mean by that? Which looks the most attractive? If you were going to play this game would you be satisfied with your level of knowledge about the probability?
This discussion should bring out that what is a good model in one context may be a poor model in a different context.
In pairs
Confirm the mean of your discrete distribution is $5, and find the standard deviation. Record your standard deviation on the board.
Graph the distribution of profit/loss in $, on x-axis, and probability as narrow bars with heights = probabilities, on y-axis.
Mark the mean, and + and – units of SD on the graph (as you would on a normal distribution). Does SD look sensible? (Is it a good measure of spread?)
Is there a relationship between the perception of risk and the standard deviation?
Extension/enrichment ideas
- Multiply all your rewards by 4. Recalculate the mean (expected value) and the standard deviation? How do these statistics compare with the original statistics?
TOP
Planned assessment
This teaching and learning activity could lead towards assessment in the following achievement standards:
Spotlight on
Pedagogy
Planning for effective learning
Planning should involve:
- starting with familiar contexts, concrete materials and prior knowledge, and moving to generalisations and abstract ideas (and back and forth between these as needed)
- using learning materials to focus student attention on key concepts.
Encouraging reflective thought and action
Examples of teacher actions that encourage reflective thought and action for students:
- Supporting students to explain and articulate their thinking.
- Encouraging students to fine-tune their statistical thinking.
Key questions that teachers can use:
- What do you notice?
- What does this make you wonder?
- What conclusions can you draw from…?
Enhancing the relevance of new learning
Examples of teacher actions that enhance the relevance of new learning:
- Providing appropriate levels of challenge.
- Encouraging students to explain their thinking.
Key competencies
Thinking
- Students use mathematics to model real life and hypothetical situations; they make conjectures, challenge assumptions and thinking, and they engage in sense making.
- Students deal with uncertainty and variation, they seek patterns and generalisations.
Relating to others
- Students share their ideas, accept a range of approaches, and respect others’ thinking.
- Students listen to others, they accept and value different viewpoints.
Values
- Students will be encouraged to value:
- innovation, inquiry, and curiosity, by thinking critically, creatively, and reflectively
- ecological sustainability, which includes care for the environment.
Māori/Pasifika
- Cooperative learning and creating knowledge together
Planning for content and language learning
Links
Last updated September 10, 2018
TOP

