Deterministic and probabilistic models
Teacher notes
Statistics includes the process of finding out about patterns in the real world using data. When solving statistical problems it is often helpful to make models of real world situations based on observations of data, assumptions about the context, and on theoretical probability. The model can then be used to make predictions, test assumptions, and solve problems.
A deterministic model does not include elements of randomness. Every time you run the model with the same initial conditions you will get the same results.
Most simple mathematical models of everyday situations are deterministic, for example, the height (h) in metres of an apple dropped from a hot air balloon at 300m could be modelled by h = - 5t2 + 300, where t is the time in seconds since the apple was dropped.
Simple statistical statements, which do not mention or consider variation, could be viewed as deterministic models. The linear regression equation in a bivariate analysis could be applied as a deterministic model if, for example, lean body mass = 0.8737(body weight) - 0.6627 is used to determine the lean body mass of an elite athlete.
A probabilistic model includes elements of randomness. Every time you run the model, you are likely to get different results, even with the same initial conditions. A probabilistic model is one which incorporates some aspect of random variation.
Deterministic models and probabilistic models for the same situation can give very different results. Consider a very simple model of a cash machine. Customers arrive to use the machine every two minutes on average. Customers take 2 minutes to use the machine on average. What is the probability that a customer has to wait 3 minutes or more?
A deterministic model of the situation just uses the average gap between customers and the average time of usage, and assumes these have no variation, that is, all gaps are 2 min, and all usage times are 2 min. The model assumes that someone arrives exactly every two minutes and uses the machine for exactly two minutes, so there is never any waiting time. The distribution of waiting times is that all waiting times are zero minutes.
A simple probabilistic model of the same situation might keep the time of use at the machine as 2 minutes for each person, but include random arrival times. One way to include randomness in the model is to do a simulation. We can simulate 15 random arrival times in a 30 minute period, for example, 2 4 5 5 10 11 12 15 16 19 20 24 29 29 29. In the table below, the customers are represented by the letters a to o, arriving to either use the machine or wait until the machine is free.
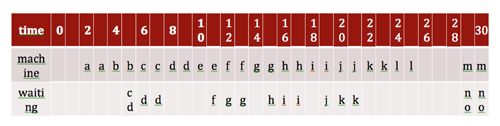
The distribution of waiting times from the simulation is:
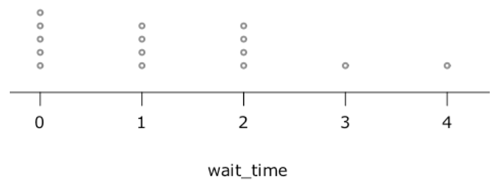
The above example uses just one small simulation. Probabilistic models can be based on experimental distributions or distribution models.
Deterministic models can be relatively simple and can be used when random variation is not a major influence on the situation being modelled (random variation is relatively small). If random variation is a major component of the context, a probabilistic model may be needed to fit the purpose. For instance, trains in Japan run on time, usually to within less than a minute of the scheduled time, so a deterministic model of expected travel time could be made using the scheduled train times. In the USA trains are often late, so a model incorporating the probability of delay could be useful.
Last updated September 24, 2013
TOP



