Achievement objective M8-11
In a range of meaningful contexts, students will be engaged in thinking mathematically and statistically. They will solve problems and model situations that require them to:
- choose and apply a variety of differentiation, integration, and anti-differentiation techniques to functions and relations, using both analytical and numerical methods.
Indicators
- Understands and uses a range of differentiation techniques including:
- first principles (only for polynomials of degree ≤ 3)
- product rule, quotient rule, chain rule
- other techniques including implicit or parametric differentiation, for example, conic relations.
Functions include:
- polynomials
- rational
- ex
- ln(x)
- trig functions
- xn, n ∈ R .
- Develops an understanding of integration by:
- using numerical methods for finding areas under curves (rectangle rule, trapezium rule, and Simpson’s rule)
- relating the definite integral to the limit of a sum (Riemann Integral)
- linking integration and anti-differentiation using the fundamental theorem of calculus, including:
- Part 1: If f is continuous on [a, b] and F(x) =
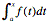for [a, b] then F'(x) = f(x) (explores using technology) (Note: this guarantees that an anti-derivative does exist for Part 2.)
- Part 2: If F' = f then
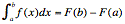
- Uses a variety of integration techniques for functions including:
- polynomials
- xn, n ∈ R
- ex
- sin(x)
- cos(x)
- f ' ( g ( x ) ) ( g ' ( x ) )
- f'(x)/f(x)
Applications include:
- finding areas under and between curves
- (related) rates of change
- kinematics
- optimisation
- points of inflection
- concavity.
- Makes links with differential equations
M8-12.
- See
key mathematical ideas on NZmaths.
Progression
M8-11 links from
M7-9,
M7-10.
TOP
Possible context elaborations
- Applications for differentiation techniques include:
- rates of change
- tangents and normals to curves
- features of graphs including turning points, points of inflection and concavity
- optimisation.
- Applications for integration techniques include:
- finding areas under and between curves
- rates of change
- kinematics.
-
Activity: 28 Days later – Zombies
Assessment for qualifications
NCEA achievement standards at levels 1, 2 and 3 have been aligned to the New Zealand Curriculum. Please ensure that you are using the correct version of the standards by going to the
NZQA website.
The NZQA subject-specific resources pages are very helpful. From there, you can find all the achievement standards and links to assessment resources, both internal and external.
The following achievement standard(s) could assess learning outcomes from this AO:
Last updated September 17, 2018
TOP
