What are graphs and networks?

Introduction

Mathematicians and others use networks and graphs to describe relationships between things or people.

Mathematics is often about how one thing relates to another or how objects in a collection can be connected. Relatedness or connection is the basis of a network.

A network or graph is just what you think it is – a collection of dots, called vertices or nodes, with some dots joined to other dots by lines, called edges or arcs.

Many practical applications

Networks and graphs have many everyday applications.

The Internet (Worldwide Web) is an example of a network or graph, as are family trees. You can use graphs to show the friends you chat to on a social network.

Graphs have practical uses, such as timetabling, scheduling flights, finding the shortest way to go from one part of a city to another using one-way streets, or showing the links in an organisation.

Definitions and terminology

There are many definitions associated with networks and graphs.

People sometimes use the same word to mean different things, for example, many authors write “graphs” when they are discussing “networks”.

The whole area of networks and graphs is usually called graph theory. This is a bit confusing as graphs can also mean the diagram or plot of a function.

The next section sets out some of the main definitions used in in the mathematics and statistics teaching and learning guide. These definitions are consistent with those most commonly used.

TOP

Definitions

Graph

A graph (G) is a set or collection of points, usually called vertices or nodes, as well as a set of edges connecting some of the vertices.

Figure 1

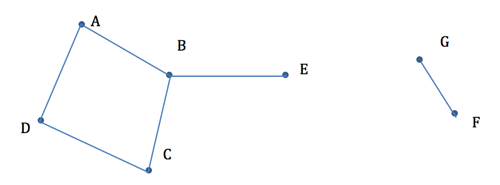
Graphs - figure 1

Figure 1 is a graph.
The vertices are A, B, C, D, E, F, and G.
The edges are AB, AD, DC, BC, BE, and GF.

The order in which the vertices or edges are listed does not matter. Also, the edge AB is the same as the edge BA. The length of the edges in the drawing of a graph usually does not mean anything. What mathematicians focus on is which vertices are joined to which other vertices. The graph can also be drawn in many different ways and still be the same graph.

For example, the graph in Figure 2 below is the same graph as in Figure 1. The point on the diagram where the edge FG crosses the edge AB is not a vertex. Usually we try to draw the graph as simply as possible, so the first graph is preferred, because it is easier to see the connections.

Figure 2

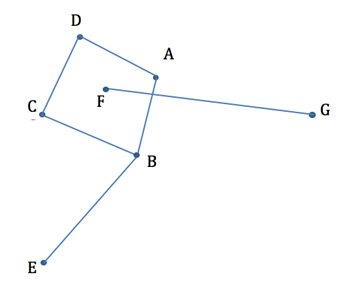
Graphs - figure 2

Loops

An edge joining a vertex to itself is a loop. If two or more edges join the same pair of vertices, they are known as multiple edges.
A graph with no loops is simple. (Unless stated otherwise, all the graphs considered in this guide will be simple.)

Figure 3

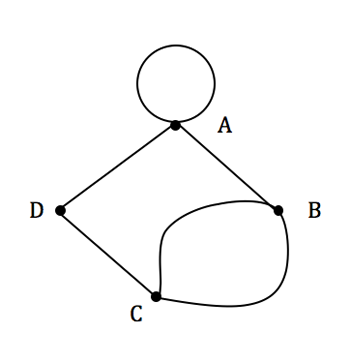
Loops - figure 3

In figure 3, the edge AA is a loop, and there are two edges joining B to C.

If an edge has an arrow on it to show a direction, it called an arc.

An arc from U to V is written (U,V) or simply UV.

A directed graph (digraph)

This is a graph in which every edge is an arc.

Adjacency

Two vertices joined by an edge are adjacent, and each vertex is incident to such an edge.
Two distinct edges meeting at a vertex are adjacent.
The degree of a vertex is the number of edges meeting at it (or incident to it).
A vertex is odd or even, depending on whether its degree is odd or even.

Look back to the graph in figure 1. In this graph, C is adjacent to B and D, has degree 2 and is an even vertex. Edge CB is adjacent to vertices C and B. C is incident to the edge CD.

Walks and connected graphs

Much of graph theory involves the study of walks of some kind.

A walk is an alternating sequence of vertices and edges (or arcs) from vertex v to vn, that is: v , e1, v1, e2, v2, … , vn in which edge ei (or arc) joins vi-1 and vi.
The number of edges in a walk is its length. In Figure 1, C, CB, B, BE, E is a walk of length two.
A walk where the first and last vertices are the same is a closed walk.
A walk in which every vertex (except perhaps the first and the last) is distinct is a path.
A cycle is a path where the first and last vertex is the same.
A walk in which each edge is distinct is a trail. A trail in which the first and last vertex is the same is a circuit.
A graph is connected if there is a path from u to v for every pair of vertices u and v in the graph. (Figure 3 shows a connected graph.)

Note: There is no standard notation for paths, cycles, trails, etc. A “cycle” may elsewhere be called a circuit. The terminology described here is that most commonly used and is maintained throughout this guide.

Weighted graphs and networks

An edge or arc is weighted if it has a number associated with it. These numbers usually represent practical things, for example, distances between towns, the cost of a telephone cable, the time to do a task, etc.
The weight of a walk, path, or graph is the sum of the weights of all edges (or arcs) in it.
A digraph with weighted arcs is a network.

Figure 4

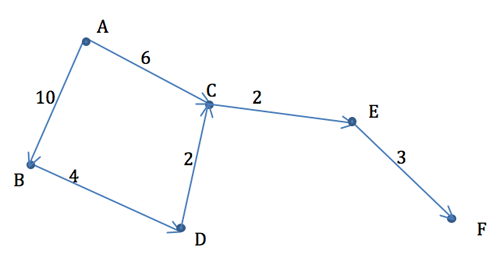
Graphs - figure 4

Figure 4 is an example of a digraph and network. Each vertex is joined to another by an arc. Each arc has a weight associated with it.

Notes:

The formal definition of a network is “a digraph with weighted arcs”. However, “network” is sometimes used loosely. This guide may refer to a graph as a network, when (strictly speaking) it is a graph, or vice versa. This shift in use can also be seen by the whole topic having the title “networks”.
Unless stated otherwise, graphs and networks in this guide will be simple and connected.

< back to AO M7-5